【解答】解:(1)∵抛物线y=ax2+bx+c与x轴交于A(5,0),B(-1,0)两点,与y轴交于点C(0,
),
∴设抛物线的解析式是y=a(x-5)(x+1)1),
则
=a×(-5)×1,解得a=-
.
则抛物线的解析式是y=-
(x-5)(x+1)=-
x2+2x+
;
(2)存在.
当点A为直角顶点时,过A作AP⊥AC交抛物线于点P,交y轴于点H,如图.
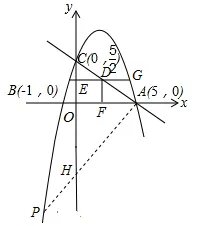
∵AC⊥AP,OC⊥OA,
∴△OAC∽△OHA,
∴
=
,
∴OA2=OC•OH,
∵OA=5,OC=
,
∴OH=10,
∴H(0,-10),A(5,0),
∴直线AP的解析式为y=2x-10,
联立
,
∴P的坐标是(-5,-20).
(3)∵DF⊥x轴,DE⊥y轴,
∴四边形OFDE为矩形,
∴EF=OD,
∴EF长度的最小值为OD长度的最小值,
当OD⊥AC时,OD长度最小,
此时S△AOC=
AC•OD=
OA•OC,
∵A(5,0),C(0,
),
∴AC=
,
∴OD=
,
∵DE⊥y轴,OD⊥AC,
∴△ODE∽△OCD,
∴
=
,
∴OD2=OE•CO,
∵CO=
,OD=
,
∴OE=2,
∴点G的纵坐标为2,
∴y=-
x2+2x+
=2,
解得x1=2-
,x2=2+
,
∴点G的坐标为(2-
,2)或(2+
,2).

